ÁLGEBRA DE BOOLE

La álgebra de boole o álgebra booleana :

La álgebra es un sistema aplicado, presentado y estudiado por George Boole en 1815, es una herramienta matemática muy utilizada para modelar los sistemas digitales, como en la electrónica digital.

En 1938 Claude Shannon propuso usar este tipo de álgebra en los sistemas digitales.

La álgebra booleana se aplica para modelar sistemas lógicos, debido a que usa las mismas variables del sistema binario 1 o 0, es decir trabaja con compuertas lógicas (AND/OR), para su operaacion se utilizan las compuertas como:

OR = Suma AND = Multiplicacion

La algebra booleana una rama especial del álgebra que se usa principalmente en electrónica digital , elemento principal usao para simplificar circuitos logicos en electronica digital.

George Boole:

(Lincoln, Reino Unido, 1815 – Ballintemple, actual Irlanda, 1864) Matemático británico, creador de un nuevo sistema de cálculo lógico que póstumamente sería llamado Álgebra de Boole. Dicho sistema, en el que las proposiciones se reducen a símbolos sobre los que puede operarse matemáticamente, supuso un avance fundamental en el desarrollo de la lógica y, más de un siglo después, hallaría un formidable e insospechado campo de aplicación en la informática y los microprocesadores, cuyo funcionamiento se basa en la lógica binaria de Boole.

Leyes de la Algebra Booleana

1) Conmutatividad:

X + Y = Y + X X · Y = Y · X

2) Asociatividad:

X + (Y + Z) = (X + Y ) + Z X · (Y · Z) = (X · Y ) · Z

3) Distributividad:

X + (Y · Z) = (X + Y ) · (X + Z) X · (Y + Z) = (X · Y ) + (X · Z)

4) Identidad:

X + 0 = X X · 1 = X

5) Complemento:

X + X(Negacion) = 1 X . X(Negacion) = 0

6) Dominacion:

X + 1 = 1 X · 0 = 0

7) Idempotencia:

X + X = X X · X = X

8) Doble complemento:

X (Doble Negacion) = X

9) Absorcion:

X + X · Y = X X · (Y + X) = X

10) De Morgan

11) Ley de absorción :

X(X + Y) = X X +( X . Y) = X

Otros

X ( X-NEGACION +Y) = X . Y

X + (X-NEGACION . Y) = X + Y

XY-NEGACION + X-NEGACION Y = X-Exclusivo Y

X-NEGACION Y-NEGACION = X EXCLUSIVO Y (Negados)

Teoremas de la Algebra de Boole

Teorema del complemento

Unico

Suponemos 2 complementos para A (A1 y A2)

A + A1 = 1 A + A2 = 1 A · A1 = 0 A · A2 = 0

A1 = A1 · 1 = A1 · (A + A2) = A1 · A + A1 · A2

A1 = 0 + A2 · A1

A1 = A · A2 + A1 · A2 = (A + A1) · A2

A1 = 1 · A2 = A2

Teorema Literal

Teorema Expresion Dual:

Esta expresion se obtiene, intercambiando las operaciones AND por OR (y vice versa), e intercambiando las constantes 0 por 1 y 1 por 0 en la expresion de conmutacion.

Por ejemplo, para la expresion de conmutacion: (A · B) + (C · D) + 0

La Expresion Dual es:

(A + B) · (C + D) · 1

Las funciones de conmutacion se pueden expresar: de Forma Algebraica, mediante una tabla de verdad o en forma Canonica.

La manera mas didactica de representar una funcion de conmutacion es mediante una Tabla de Verdad, ya que en ella se muestran los valores de salida para cada combinacion de valor de entrada. Las Tablas de Verdad permiten modelar los Sistemas Combinacionales.

TABLAS DE VERDAD EN LA ALGEBRA DE BOOLE

La tabla de verdad es una representación del comportambiento de una función logica, dependiendo del valor particular que puedan tomar cada una de sus variables. En ella se configuran las combinaciones entre variables, para cada una de ellas aparecera el valor de funcion.

Las tablas de verdada se aplican respondiendo a :

# FIlLA DE TABLA = 2 x # Variables

SIMPLIFICACION USANDO ALGEBRA DE BOOLE

FORMA CANONICA

En Álgebra booleana, se conoce como término canónico de una función lógica a todo producto o suma en la cual aparecen todas las variables en su forma directa o inversa. Una Función lógica que está compuesta por operador lógico puede ser expresada en forma canónica usando los conceptos de minterm y maxterm. Todas las funciones lógicas son expresables en forma canónica, tanto como una «suma de minterms» como «producto de maxterms». Esto permite un mejor análisis para la simplificación de dichas funciones, lo que es de gran importancia para la minimización de circuitos digitales.

Una función booleana expresada como una disyunción lógica (OR) de minterms es usualmente conocida la «suma de productos«, y su Dual de Morgan es el «producto de sumas«, la cual es una función expresada como una conjunción lógica (AND) de maxterms.

MINTERMS : MINIMO TERMINOS

MAXTERMS: MAXIMO TERMINOS

SIMPLIFICACION DE FUNCIONES

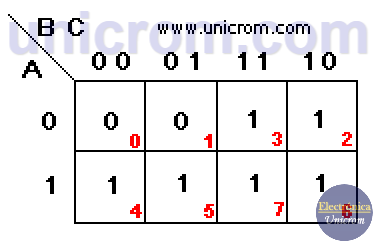
MAPAS DE KARNAUGH

Los Mapas de Karnaugh son una herramienta muy utilizada para la simplificación de circuitos lógicos. Cuando se tiene una función lógica con su tabla de verdad y se desea implementar esa función de la manera más económica posible se utiliza este método.

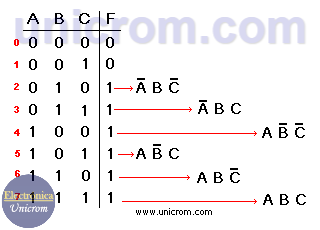
Ejemplo: Se tiene la siguiente tabla de verdad para tres variables. Se desarrolla la función lógica basada en ella. (primera forma canónica). Ver que en la fórmula se incluyen solamente las variables (A, B, C) cuando F cuando es igual a “1”. Si A en la tabla de verdad es “0” se pone A, si B = “1” se pone B, Si C = “0” se pone C, etc.