COMPUERTAS LÓGICAS

Concepto:

Se determina compuertas lógicas a los dispositivos que operan Estados Lógicos (Proposiciones), ingresa la información, se interpreta y es transformada a una puerta lógica, es decir se implementan funciones representadas mediante puertas lógicas.

La informacion procesada a traves de las compuertas logicas pueden ser calificadas como verdaderas o falsas, si es verdadera se presenta con 1 y si es falsa se representa con 0.

0 = Significa circuito abierto, no se podra poner en marcha.

1 = Significa circuito en cerrado, circuito en marcha.

Las Compuertas Lógicas son circuitos electrónicos conformados internamente por transistores que se encuentran con arreglos especiales con los que otorgan señales de voltaje como resultado o una salida de forma booleana, están obtenidos por operaciones lógicas binarias (suma, multiplicación). También niegan, afirman, incluyen o excluyen según sus propiedades lógicas. Estas compuertas se pueden aplicar en otras áreas de la ciencia como mecánica, hidráulica o neumática.

Existen diferentes tipos de compuertas y algunas de estas son más complejas, con la posibilidad de ser simuladas por compuertas más sencillas. Todas estas tienen tablas de verdad que explican los comportamientos en los resultados que otorga, dependiendo del valor booleano que tenga en cada una de sus entradas.

CONVERSION DE CIRCUITOS ELECTRICOS A CIRCUITOS LOGICOS

Definicion:

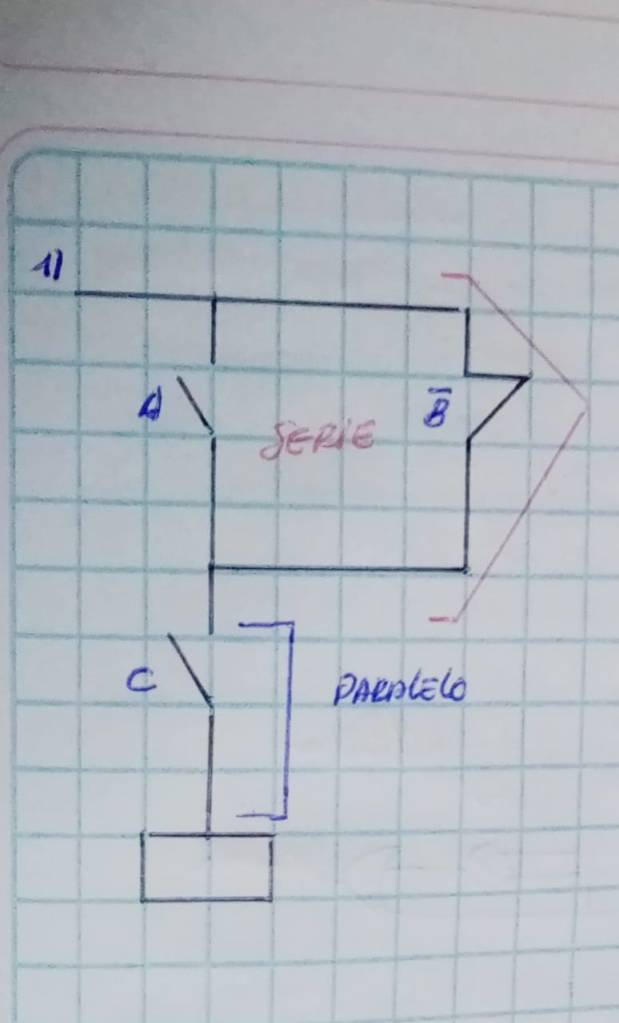
En electricidad se operan los circuitos con dispositivos electricos, electromecanicos interconectados dentro de un circuito cerrado, el circuito electrico es plasmado en un documento fisico, se emplean tramos de trayectoria abiertos o cerrados de tal manera estos circuitos pueden ser reemplazados por puertas logicas.

En eletronica digital se emplean puertas logicas, que unidas en conjunto, crean un circuito logico cerrado, las puertas logicas tambien son representadas con simbolos bajo su respectiva funcion , es decir se puede reemplazzar la trayectoria de un circuito electrico con las compuertas logicas, sabiendo interpretar los tramos abiertos o cerrados, por los simbolos de las puertas logicas

SISTEMAS DE NUMERACION

Un sistema de numeración es un conjunto de símbolos y reglas de generación que permiten construir todos los números válidos. Un sistema de numeración puede representarse como: o

N = ( S, R )

N = es el sistema de numeración considerado (p.ej. decimal, binario, hexadecimal, etc.).

S =  es el conjunto de símbolos permitidos en el sistema. En el caso del sistema decimal son {0,1,…9}; en el binario son {0,1}; en el octal son {0,1,…7}; en el hexadecimal son {0,1,…9,A,B,C,D,E,F}.

R =  son las reglas que nos indican qué números y qué operaciones son válidos en el sistema, y cuáles no. En un sistema de numeración posicional las reglas son bastante simples, que la numeración romana requiere reglas algo más elaboradas.

Estas reglas son diferentes, para cada sistema de numeración considerado, pero una regla común a todos es que para construir números válidos en un sistema de numeración determinado sólo se pueden utilizar los símbolos permitidos en ese sistema. Para indicar en qué sistema de numeración se representa una cantidad se añade como subíndice a la derecha el número de símbolos que se pueden representar en dicho sistema.

Sistema de numeracion posicionales :

El número de símbolos permitidos en un sistema de numeración posicional se conoce como base del sistema de numeración. Si un sistema de numeración posicional tiene base b significa que disponemos de b símbolos diferentes para escribir los números, y que b unidades forman una unidad de orden superior.Ejemplo en el sistema de numeración decimal

Si contamos desde 0, incrementando una unidad cada vez, al llegar a 9 unidades, hemos agotado los símbolos disponibles, y si queremos seguir contando no disponemos de un nuevo símbolo para representar la cantidad que hemos contado. Por tanto añadimos una nueva columna a la izquierda del número, reutilizamos los símbolos de que disponemos, decimos que tenemos una unidad de primer orden (decena), ponemos a cero las unidades, y seguimos contando.

De igual forma, cuando contamos hasta 99, hemos agotado los símbolos disponibles para las dos columnas; por tanto si contamos (sumamos) una unidad más, debemos poner a cero la columna de la derecha y sumar 1 a la de la izquierda (decenas). Pero la columna de la izquierda ya ha agotado los símbolos disponibles, así que la ponemos a cero, y sumamos 1 a la siguiente columna (centena). Como resultado nos queda que 99+1=100.

• Binario o Base 2 (0, 1)
• Octal o Base 8 (0, 1, 2, 3, 4, 5, 6, 7)
• Hexadecimal o Base 16 (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F)
• Decimal o Base 10 (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)

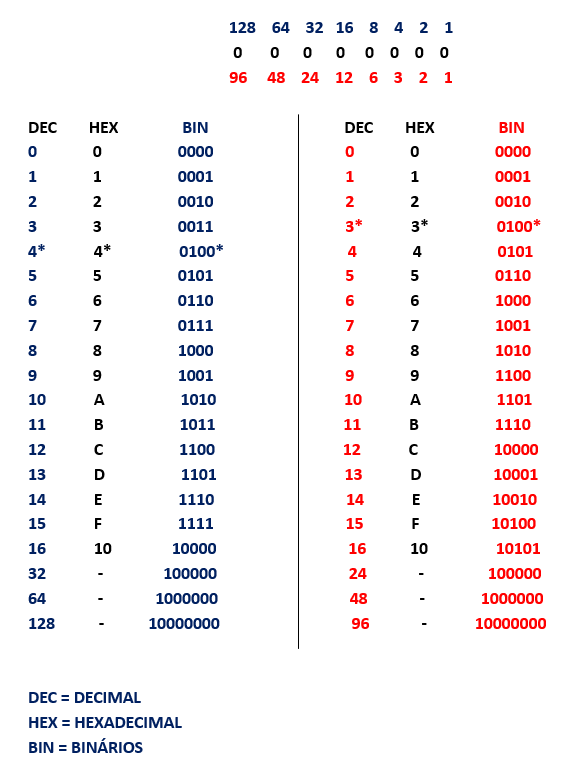
SISTEMA BINARIO

El sistema binario es el sistema de numeración que cuenta con sólo dos números: 0 y 1. Por lo que utiliza la base 2. En otras palabras, es una manera de escribir los números naturales con sólo los números 0 ó 1.

Es un sistema posicional: los enteros se escriben de 0 y 1, pero la importancia del 1 depende de la posición del número: el número 1 puede representar uno, dos, cuatro, ocho, dieciséis.

• El número cero se escribe como 0;
• El número uno se escribe como 1;
• El número dos se escribe 10
• El número tres se escribe como 11;

En términos generales, para «traducir» en sistema decimal un entero escrito en sistema binario, procedemos de la siguiente manera:

• Se escriben debajo de cada cifra las potencias crecientes de 2, partiendo de la derecha; 2⁰, 2 ¹, 2 ², 2 ³…
• Se suman las potencias de 2 escritas bajo las cifras 1.

En el sistema binario solo se necesitan dos cifras.

El valor numérico representado en cada caso depende del valor asignado a cada símbolo. En una computadora, los valores numéricos pueden representar dos voltajes diferentes; también pueden indicar polaridades magnéticas sobre un disco magnético. Un «positivo», «sí», o «sobre el estado» no es necesariamente el equivalente al valor numérico de uno; esto depende de la nomenclatura usada.

De acuerdo con la representación más habitual, que es usando números arábigos, los números binarios comúnmente son escritos usando los símbolos 0 y 1. Los números binarios se escriben a menudo con subíndices, prefijos o sufijos para indicar su base. Las notaciones siguientes son equivalentes:

• 100101 binario (declaración explícita de formato)
• 100101b (un sufijo que indica formato binario)
• 100101B (un sufijo que indica formato binario)
• bin 100101 (un prefijo que indica formato binario)
• 100101₂ (un subíndice que indica base 2 (binaria) notación)
• %100101 (un prefijo que indica formato binario)
• 0b100101 (un prefijo que indica formato binario, común en lenguajes de programación)

CONVERSION DE SISTEMA BINARIO A DECIMAL

De binario a decimal

En sistema decimal, las cifras que componen un número son las cantidades que están multiplicando a las distintas potencias de diez (10, 100, 1000, 10000, etc.)

Por ejemplo, 745 = 7 · 100 + 4 · 10 + 5 · 1
O lo que es lo mismo: 745 = 7 · 10² + 4 · 10¹ + 5 · 10⁰

En el sistema binario, las cifras que componen el número multiplican a las potencias de dos (1, 2, 4, 8, 16, ….)
         2⁰=1, 2¹=2, 2²=4, 2³=8, 2⁴=16, 2⁵=32, 2⁶=64, …

Por ejemplo, para pasar a binario un número decimal, empezamos por la derecha y vamos multiplicando cada cifra por las sucesivas potencias de 2, avanzando hacia la izquierda:

10110₂ = 0 · 1 +  1 · 2 + 1 · 4 + 0 · 8 + 1 · 16 =  2 + 4 + 16 = 22₁₀
110₂ = 0 · 1 + 1 · 2 + 1 · 4 = 2 + 4 = 6₁₀

CONVERSION DE DECIMAL A BINARIO

Se divide el número del sistema decimal entre 2, cuyo resultado entero se vuelve a dividir entre 2, y así sucesivamente hasta que el dividendo sea menor que el divisor, 2. Es decir, cuando el número a dividir sea 1 finaliza la división.
A continuación se ordenan los restos empezando desde el último al primero, simplemente se colocan en orden inverso a como aparecen en la división, se les da la vuelta. Éste será el número binario que buscamos.

Ejemplo: Transformar el número decimal 131 en binario. El método es muy simple:

131 dividido entre 2 da 65 y el resto es igual a 1
65 dividido entre 2 da 32 y el resto es igual a 1
32 dividido entre 2 da 16 y el resto es igual a 0
16 dividido entre 2 da 8 y el resto es igual a 0
8 dividido entre 2 da 4 y el resto es igual a 0
4 dividido entre 2 da 2 y el resto es igual a 0
2 dividido entre 2 da 1 y el resto es igual a 0
1 dividido entre 2 da 0 y el resto es igual a 1

-> Ordenamos los restos, del último al primero: 10000011

En sistema binario, 131 se escribe 10000011

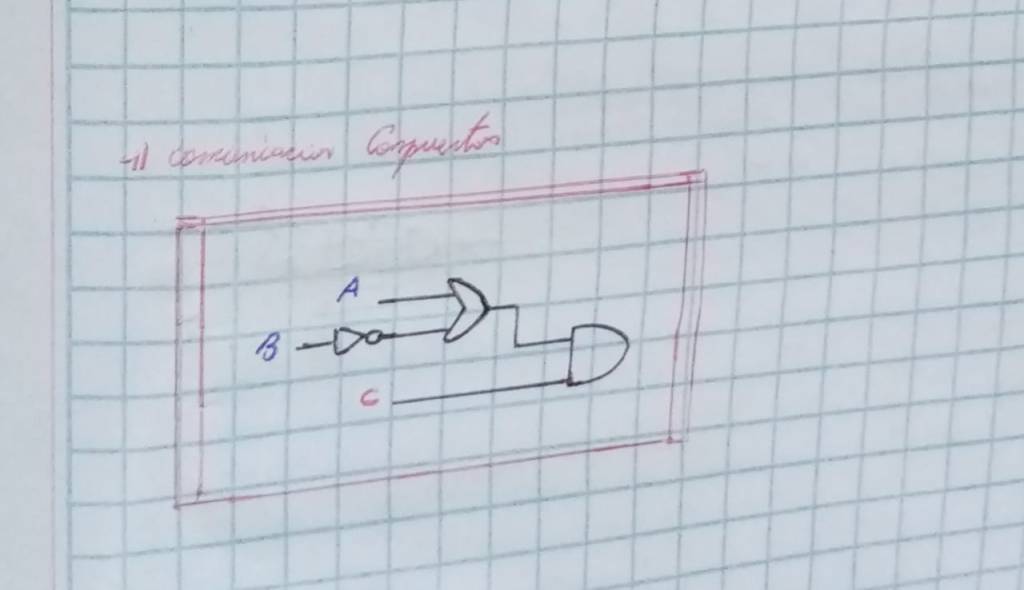
COMPUERTAS LOGICAS

Compuerta AND

La siguiente tabla muestra el símbolo de circuito y las combinaciones lógicas para una AND Gate. (En el símbolo, los terminales de entrada están a la izquierda y el terminal de salida está a la derecha.) La salida es “true ” cuando ambas entradas son “true. ” de lo contrario, la salida es “false. ”

La expresión booleana para la operación AND es Y = A . B

Compuerta OR

La puerta OR recibe su nombre por el hecho de que se comporta de acuerdo con la forma de la lógica inclusiva “o”. La salida es “verdadera” si una o ambas entradas son “verdaderas”. Si ambas entradas son “falsas”, entonces la salida es “falsa”.

La expresión booleana para la operación OR es Y = A + B

Compuerta NOT

Un inversor lógico, a veces llamado puerta NOT para diferenciarlo de otros tipos de dispositivos inversores electrónicos, tiene solo una entrada. Sirve para invertir el estado lógico.

Compuerta NOR

Es una combinación de la compuerta OR seguida de un inversor. Su salida es “verdadera” si ambas entradas son “falsas”. De lo contrario, la salida es “falsa”.

Compuerta NAND

Funciona como una la puerta AND seguida por una puerta NOT. Actúa en la forma de la operación lógica “y ” seguida de negación. La salida es “false ” si ambas entradas son “true. ” de lo contrario, la salida es “true. ”

Compuerta XOR

(exclusivo-OR) actúa de la misma manera que la lógica “o / o”. La salida es “verdadera” si cualquiera de las entradas es “verdadera”. La salida es “falsa” si ambas entradas son “falsas” o si ambas entradas son “verdaderas”. Otra forma de ver este circuito es observar que la salida es (uno) si las entradas son diferentes, pero (cero) si las entradas son las mismas.

Compuerta XNOR

(exclusive-NOR) es una compuerta XOR combinada seguida por un inversor. Su salida es “verdadera” si las entradas son iguales, y “falsa” si las entradas son diferentes.

Usando las combinaciones de compuertas lógicas, se pueden realizar operaciones complejas. En teoría, no hay límite para el número de puertas que se pueden organizar juntas en un solo dispositivo. Pero en la práctica, hay un límite para la cantidad de puertas que se pueden empaquetar en un espacio físico determinado.

TABLA DE VERDAD

Una aplicación importante de las tablas de verdad procede del hecho de que, interpretando los valores lógicos de verdad como 1 y 0 (lógica positiva) en el sentido que

• valor «1» permite el paso de corriente eléctrica; y
• valor «0» corta el paso de dicha corriente.

Los valores de entrada o no entrada de corriente a través de un diodo pueden producir una salida 0 ó 1 según las condiciones definidas como función según las tablas mostradas anteriormente.

Así se establecen las algunas funciones básicas: AND, NAND, OR, NOR, XOR, XNOR (o NXOR), que se corresponden con las funciones definidas en las columnas 8, 9, 2, 15, 10 y 7 respectivamente, y la función NOT.

En lugar de variables proposicionales, considerando las posibles entradas como EA y EB, podemos armar una tabla análoga de 16 funciones como la presentada arriba, con sus equivalentes en lógica de circuitos.